I came across the following example challenge from Project Euler on freeCodeCamp‘s website and it seemed that Collatz sequence generation in Python would prove to be a worthy test of our programming meddle.
Instructions are as follows:
The following iterative sequence is defined for the positive set of integers:
$n \rightarrow n/2$, if $n$ is even, $n \rightarrow 3n + 1$, if $n$ is odd Using the rule above and starting with 13, we generate the following sequence:
$$ 13 \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 $$It can be seen that this sequence (starting at 13 and finishing at 1) contains 10 terms. Although it has not been proved yet (Collatz problem), it is thought that all starting numbers finish at 1.
Which starting number, under one million, produces the longest chain?
Generating the Collatz sequence: a first stab
Owing to how they are defined, Collatz sequences can be generated by a recursive algorithm comprised of only a few simple, thoughtfully placed, operations. Let’s see if we can do that here:
# Collatz conjecture Project Euler example
def collatz(seq):
# seq must be an integer greater than 0 or
# a list of intergers all of which are
# greater than 0
if type(seq) == int:
seq = [seq] # insert int arg into list
if seq[-1] == 1: # recursion termination path
pass # exit clause if last
# element is 1
else: # build sequence via recursion
if seq[-1]%2 == 0: # if last element is even
seq.append(int(seq[-1]/2)) # divide by 2
collatz(seq) # and append result, self-call
# with updated list as arg.
else: # alternatively, if last element is odd
seq.append(int(3*seq[-1] + 1)) # mult. by 3
collatz(seq) # and add 1, append result,
# self-call with updated list
# as arg.
return seq # set output to be entire list
collatz(13)
Yep, it works.
But truth be told, I’m less than thrilled with the type-conversion and list-append operations. How about we try to work out something a bit more elegant.
A more refined Collatz sequence generator
Instead of using a list, we can unpack a tuple of the sequence in the function’s argument definition. This permits us to insert each new sequence entry by including it as the last argument in a recursive self-call. Employing this approach, we eliminate the separate list-append operation that we were forced to use in the previous version. But just as before, the sequence grows by one more element with each recursive step until self-calls are by-passed when the last entry equals 1.
# A more elegant Collatz constructor
def collatz2(*seq):
# seq must be an integer greater than 0 or
# a sequence of intergers all of which are
# greater than 0
if seq[-1] == 1: # terminate recursion if
pass # last element is 1
else: # build sequence via recursion
if seq[-1]%2 == 0: # case: last element even
# include n/2 result as last argument
# of self call
seq = collatz2(*seq, int(seq[-1]/2))
else: # case: last element odd
# include 3n+1 result as last argument
# of self call
seq = collatz2(*seq, int(3*seq[-1] + 1))
return seq # set output to be entire sequence.
Reproduce example sequence
Alright, now that we’ve defined our refined Collatz generator, let’s verify that it reproduces the sequence given in the instructions above.collatz2(13)
Goody gumdrops; it does.
Let’s try another starting integer, say, after switching digit position. This time, for the sake of brevity, let’s just examine some meta properties of the generated sequence.
collatzList = collatz2(31)
print('Number of elements in sequence: {}'.format(len(collatzList)))
print('Last number in sequence (should be 1): {}'.format(collatzList[-1]))
print('Finally, how about the largest number in the sequence: {}'.format(max(collatzList)))
Yowza!
In this case, the Collatz sequence contains a number that is two orders of magnitude larger than the number we started with! We would do well to remember this as we move forward.
Onto the challenge…
Testing the waters
Before unleashing this beast on integers approaching one million, let’s first find out the maximum size integer that our machine and Python can handle.
import sys
print('Maxiumum integer that can be processed by our machine: {:.5E}'.format(sys.maxsize + 1))
Yeah our maximum-allowable integer seems to be pretty-darn-large despite our admittedly lack-lustre setup. Note, however, that integers in a Collatz sequence can be orders of magnitude larger than the starting number. Recall the sequence for integer 31 above; it had an integer >9000 in its sequence. Even so, ~9E18 should be large enough (famous last words…) for a sequence that starts around 1e6–hopefully 12 orders of magnitude is sufficient space for intermediate values of the sequence to grow as need be. Let’s at least keep our fingers crossed, though, when we call our generator with arguments valued in this neighborhood.
import time
for i in range(-1,2):
start = time.time()
collatzList = collatz2(1e6+i)
duration = time.time() - start
print('It took {:.5} seconds to generate the Collatz sequence for {}.'.format(
duration, int(1e6+i)))
print('The sequence contains {} elements'.format(len(collatzList)))
No sweat.
No fan revving up, and no never-ceasing cyclic processing indicators to speak of; definitely a good sign.
A processing time on the order of 1 millsecond per high-valued integer should not be prohibitive, in terms of time, for a brute force search to find the number with the longest Collatz sequence in domain [1, 1E6). (There’s that “should” again.)
Based on these measurements, and using a convenient figure between extremes, one million numbers, that each take around, say, 1 millisecond to process, would mean a total duration of about 1e3 seconds (less than 17 minutes).
Again, this is a very loose figure to estimate the overall time to compute all Collatz sequences over the entire domain. Please remember that we expect that for some integers processing will take much longer than 1 millisecond, and for others, their Collatz sequences can be computed much faster, as we see above. My guess: 17 minutes is likely an overestimate considering that we timed numbers at the high end of the domain.
Now let’s compare our estimate to actual.
Iterate over domain and record sequence lengths
# Which number under 1E6 produces the longest chain?
# Brute force search??? It could take a while...
start = time.time()
collatzList = [[len(collatz2(n)), n] for n in range(1,int(1e6))]
duration = time.time() - start
print('It took {:.5} seconds to generate the Collatz sequences over [1,1e6).'.format(
duration))
Woops. For those of you who’d prefer a processing time in human-interpretable units: 213 seconds is about 3.5 minutes.
Not all that bad of a wait considering our estimate of 17 minutes above.
Find longest sequence and its starting integer
All that is left to do now is select the longest tuple and corresponding starting integer.
longest = max(collatzList)
print('The longest Collatz sequence is comprised of {} elements for number {}'.format(
longest[0], longest[1]))
And there you have it.
Just for kicks: plot stop times
While we’re here, and have at our fingertips a large array of Collatz sequence lengths, how about we make ourselves a nifty banner graphic for his post?
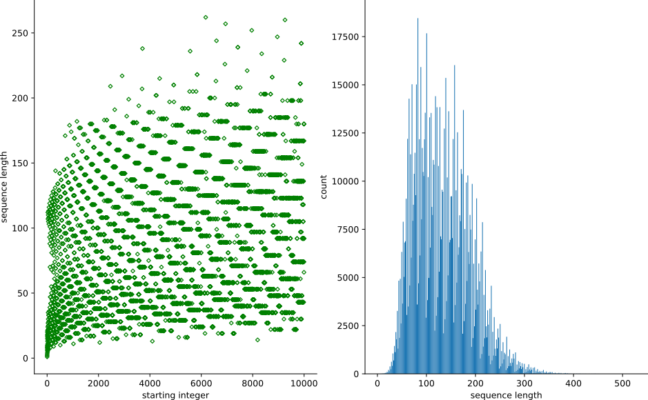
Below, we generate a scatter plot of Collatz stop times (sequence lengths) for integers in the domain [1, 1e4].
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.figure
import matplotlib.axes
fig, ax = plt.subplots(nrows=1, ncols=2)
fig.set_size_inches(11,7)
plt.tight_layout(pad=2.5)
clArray = np.array(collatzList)
ax[0].scatter(clArray[0:9999,1], clArray[0:9999,0],
color='green', marker='D', s=10, facecolors='none')
ax[0].set_ylabel('sequence length')
ax[0].set_xlabel('starting integer')
ax[1].hist(clArray2[:,0], bins=n_bins)
ax[1].set_xlabel('sequence length')
ax[1].set_ylabel('count')
#ax[1].ticklabel_format(axis='y', style='scientific')
Kinda purdy…
Notice the widening, curved striations in the left plot, as well as oscillating bin heights in the histogram on the right. To me, this apparent structure indicates some underlying pattern pulling strings behind the progression of Collatz sequences. Well, as inviting as it may be to find one, no one has yet. The Collatz Conjecture remains unproven.
fig.savefig('CollatzStopTimesPlotAndHisto.svg')