Contents
Overview
Last time, in part two, we built and tested our set container class, ModSet(), with a variety of methods that will prove useful when we construct the power set. Methods included copying, nesting/unnesting, filtering to keep only unique members as well as set-union and set-subtraction operations. You will see that most of these will be used, either implicitly or explicitly, in both Binary Mask and Recursive methods of generating power sets.
Preliminaries
Our ModSet() class definition is a must (obviously); let’s run its script so it will be ready and waiting for us when it comes time to make an instance. You can download the script from github here: modset.py
%run modset.py
When we are ready to build our power set, we’ll measure the time it takes each of the two routines to complete, so we can compare their performance. As a preliminary, let’s import the time module so it stands at ready.
import time
Of course we will need an example source set to operate on. Let’s define it now and be done with it.
clumsyPrez = ModSet(set([ 6.1, 2021, "fight like hell", "we love you",('impeachment','#2')]))
Binary Mask power set generator
In this iterative-based approach, we will populate the power set by applying binary masks to extract out member subsets, one-by-one, from the source set in ModSet().val. If you recall, a verbal description of power set generation using a binary mask we discussed way back in part one; you can find it here. Below, we first provide an overview of our binary mask power set generator routine, followed by the routine itself, with heavy commenting, concluded with a detailed walk-through after that.
Overview
The method, named .powerSet_bin(), contains 19 lines and calls .pushDown() and .union() sibling methods. Though we could use NumPy here to make mask generation and member extraction more compact, we did not want to confound the comparison (to our recursive approach to follow) by incorporating functionality of an external module. Already, the code has been somewhat compressed by use of generator expressions.
Flow of control
The routine below can be divided into two main blocks: variable initialization, and the run-time loop that builds each binary mask for extracting the corresponding subset on each iteration. The loop populates the power set member-by-member and terminates when all $2^n$ members have been added. Because indexing is crucial in this approach, you’ll notice heavy use of range() and list() data-types. As you’ll see later, our recursive approach requires no such crutch.
class ModSet():
.
.
.
# Generate powerset via direct, binary mask approach
def powerSet_bin(self):
## Initialize local variables ##
S = list(self.val) # convert to list for indexing
setSize = len(self.val) # count number of members in source set
psetSize = pow(2, setSize) # calculate the number of elements in the power set
lastIndex = setSize - 1 # index value of last member
setIndices = range(0, setSize) # make indices list for source set
psetIndices = range(0, psetSize) # make indices list for power set to be built
bMasks = [[False for s in setIndices] for p in psetIndices] # Initialize binary mask
pSet = ModSet(set()) # initialize power set as empty ModSet() instance
pSet.pushDown(1) # and nest it down one level for later joining
## Populate powerset with each subset, one at a time ##
for i in psetIndices: # loop through each member of power set
## Generate binary mask for subset i of power set ##
val = i # assign current pSet index as current "value" of mask
for j in setIndices: # loop through each bit-digit of mask
if (val >= pow(2, lastIndex - j)): # if mask value >= value of current bit,
bMasks[i][lastIndex - j] = True # then set corresp. mask bit to "true"
val -= pow(2, lastIndex - j) # subtract value of current bit from
# mask value to determine next bit-digit
## Form subset i of power set ##
# Use generator expression for compactness
dummySet = ModSet(set([S[k] for k in setIndices if bMasks[i][k] == True]))
dummySet.pushDown(1) # nest ModSet instance down one level for union join
pSet.union(dummySet) # include new subset in power set
return pSet, bMasks # return complete power set and binary masks as output
Aside: initializing the mask
To have each and every element alterable in our list of binary masks, bMasks, we need to individually assign each and every element within the nested list. If you attempt to initialize bMasks like this, bMasks = [[False]*len(setIndices)]*len(psetIndices)], (as we did on our first attempt!), you will find that you cannot change individual elements of bMasks later on. That is
bMasks =[[False]*3]*5
bMasks[3][1] = True
bMasks
changes to True all row-entries in the second column, rather than just the fourth, since all point to the same instance of True. However, if you initialize bMasks using a list completion, the nested list assembles with a hash to a unique instance for each and every element therein
bMasks = [[False for j in range(0,3)] for i in range(0, 5)]
bMasks[3][1] = True
bMasks
so that we can make the individual bit flips necessary for our routine. Our apologies for the digression; we felt the need to address this “rookie” Python mistake for those who may be unaccustomed to using list objects in this, possibly unusual, manner.
Testing the binary mask routine
With the binary mask routine complete, we’re ready to build our power set. Below we’ve sandwiched the call within two time.time() reads, so we can measure its runtime duration. Let’s examine bMasks output first.
tStart = time.time() # clock start timestamp
pSet_bin, bMasks = clumsyPrez.powerSet_bin() # call our binary mask power set generator
duration = time.time() - tStart # calc run duration by subtracting tStart from current time.
bMasks # show list of binary masks
Above, you can see that masks progress from all False to all True in a logical pattern. This ordering would be a great feature if we cared about how members are ordered in our power set. But sets, strictly defined, are not distinguished by the ordering of their members (Van Dalen, Doets, De Swart; 2014). That is, set $\{a, b, c\}$ is equivalent to set $\{c, a, b\}$ and $\{b, a, c\}$, and so on.
So, after taking a look at our power set in pSet_bin, we see that the nice ordering was all for naught.
# Report duration of binary mask power set generation
print('The Binary Mask approach took %0.6f seconds to complete.'%(duration))
print('The power set contains %i subset elements'%(len(pSet_bin.val)))
pSet_bin.val # show power set output; remember, this is a set!
From the power set output string above, it looks like we have many sub-set instances as members of one big super-set. But, if you recall from all the way back in part one, this is not the case; our power set pSet_bin is actually a ModSet() object, whose .val attribute is a set, each element of which is another ModSet() instance that contains one unique sub-set of the original source set (as its .val attribute). We defined the ModSet.__repr__() method to return the code representation of its .val attribute; that’s the reason why the return string from calling pSet_bin.val appears in this set-resembling format.
Recursive power set generator
Overview
Our recursion-based method for generating power sets contains just 11 lines of code but requires five sibling methods, as well as itself, to run. Though .powerSet_rec() has fewer lines than .powerSet_bin(), it relies more heavily upon behavior of sibling methods in the ModSet() class, i.e. .__copy__(), .pushDown(), .diffFunc(), .union() and .removeDuplicates() to perform the respective obligatory processing tasks of duplication, nesting, extraction, joining and filtering. Unlike the Binary Mask approach above, indexing is not needed here, and hence, not employed. Through recursion, we can generate the identical power set using thoughtfully-placed set-subtraction, -union and -filtering operations.
class ModSet():
.
.
.
# Generate power set recursively.
def powerSet_rec(self):
pSet = self.__copy__() # Preserve self instance; its copy, pSet
# will be altered
pSet.pushDown(1) # Nest pSet for later joining.
if len(self.val) > 0: # Recursion termination condition
for elSet in self.val: # Iterate through members of set self.val
# Generate subset that remains after removing current
# element, elSet, from set self.val
dummySet = self.diffFunc(ModSet(set([elSet])))
# To current powerset, append the powerset of the
# subset from previous step
pSet.union(dummySet.powerSet_rec()) # Self-call power set method,
# union join power set of
# dummySet with pSet
return pSet # Return power set at current
# level of recursion
else:
dummySet = ModSet(set()) # Generate instance of ModSet of empty set
dummySet.pushDown(1) # Nest empty set down one level so it can
return dummySet # be union-joined in the recursion level
# above (that called this current run).
Flow of control
First a duplicate of the calling instance is made to serve as the (local) power set within our routine. This instance is promptly pushed down one level so it can be joined by union later, if necessary. Next, the number of elements in the calling instance are counted. If empty, an empty ModSet() instance is returned on exit of the routine. This case path is the exit condition for the recursive flow; eventually all calling instances will dwindle down to empty as members are stripped from them in the alternative, non-empty, case that we’ll describe next.
If the calling instance is not empty, .powerSet_rec() iterates over the elements therein, each time subtracting out the current element, elSet, and calling itself again to build the power set from elements that remain. Output from this recursive call is then joined by union with pSet. Remember that every time pSet.union() runs, it calls the filtering method removeDuplicates() to retain only unique members in pSet as it is assembled.
When the loop completes, and all subsets have been included at the present level, the local instance of pSet is returned so that it can be union-joined with the pSet instance inside the calling-function one level above. The method continues in this fashion until pSet at the top-most level of recursion is fully populated, at which point output is returned in response to the initial method call.
[Phew..!]
Let’s give it a whirl and gauge its run-time duration.
Testing the recursive routine
tStart = time.time()
pSet_rec = clumsyPrez.powerSet_rec()
duration = time.time() - tStart
print('The Recursive approach took %0.6f seconds to complete.'%(duration))
print('The power set contains %i subset elements'%(len(pSet_rec.val)))
pSet_rec.val
As promised, we see the same power set as we saw from the Binary Mask approach. But unlike that approach, there is no mask output for us to examine this time.
Quick-and-dirty efficiency comparison
For a given programming objective, recursive algorithms tend to be less efficient than their iterative equivalents when used in imperative-based languages, like Python, where iteration is preferred (Recursion (computer science), Wikipedia). Below we hobbled together a quick script to measure, and statistically compare, processing times of the two methods of power set generation of clumsyPrez. We instruct the two power set generators to each run 500 times in a randomly alternating sequence to destroy potential processing-related biases (e.g. sequential, timing) that could otherwise arise by running the two in separate blocks.
import numpy as np
import matplotlib.pyplot as plt
# routine to repeatedly collect run-time durations
# of functions genFunc1 and genFunc2
def genDurationsDist(genFunc1, genFunc2, nReps):
durations = np.zeros(2*nReps) # initialize output array
genFuncs = [genFunc1, genFunc2] # make list of the two functions to run
# initialize an array to contain the run-sequence of the two functions
funcSeq = np.concatenate([np.zeros(nReps), np.ones(nReps)]).astype(int)
np.random.shuffle(funcSeq) # shuffle the ordering of the sequence
for i in np.arange(0, funcSeq.shape[0]): # iterate over random sequence
tStart = time.time() # start timestamp
genFuncs[funcSeq[i]]() # run one of the two functions based on funcSeq
durations[i] = time.time() - tStart # end timestamp, calc duration
# separate and return the two sets of durations
return durations[funcSeq == 0], durations[funcSeq == 1]
durations_bin, durations_rec = genDurationsDist(clumsyPrez.powerSet_bin,
clumsyPrez.powerSet_rec, 500)
Now that we have distributions of processing times from the two power set generators, we can plot histograms and Q-Q plots to get an idea of their locations and shapes.
import nonparametric_stats as nps
plt.rcParams['figure.figsize'] = [7, 5]
durs = (10**3)*np.array([durations_bin, durations_rec])
# Obtain color cycle that matplotlib uses
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
# plot histograms of duration distributions
labels=['Bin. Mask', 'Recursive']
ax = nps.histPlotter(50, *durs, labels=labels, colors=colors)
ax.set_title('Runtime durations of 2 power set generators')
ax.set_xlabel('duration (msec.)')
ax.set_ylabel('counts')
ax.legend()
# Examine Q-Q plots to compare distributions to
# their corresponding theoretical normal dists
fig, axs = plt.subplots(nrows=1, ncols=2)
fig.tight_layout()
for i in range(0,2):
nps.qqPlotter_normal(durs[i], 30, axes=axs[i], color=colors[i])
axs[i].set_title(labels[i] + ' gen. Q-Q')
axs[i].set_xlabel('theoretical normal')
if i == 0:
axs[i].set_ylabel('data')
The two distributions certainly do not appear to be normally distributed; they depart from Normal theoretical very early on. Consequently the typical two-tailed Student t-test cannot be used here. Below, we import and run the Mann-Whitney non-parametric comparison test to assess if the difference between the two reaches statistical significance.
from scipy.stats import mannwhitneyu as mwu
med_bin = (10**3)*np.median(durations_bin) # compute median duration of Bin. Mask ps durations
med_rec = (10**3)*np.median(durations_rec) # compute median duration of Recursive ps durations
print('Median Bin. Mask duration: %0.2f msec., Median Recursive duration: %0.2f msec.'\
%(med_bin, med_rec))
# Run non-parametric test to determine if differences between
# distributions are statistically significant
uStat, pVal = mwu(durations_bin, durations_rec)
print('Mann-Whitney U statistic: %0.2f, p-value: %0.2e'%(uStat, pVal))
Measuring the time elapsed for each of the two approaches, we find that, on average, our recursive algorithm does indeed take about twice the time to complete on our machine as the binary-mask method (4.59 ms versus 2.11 ms, U = 487, p < 0.01). Of course, ours is certainly not a very controlled comparison; so please take the result with “a grain of salt” if you will.
Summary
In part one we discussed power sets and their relation to the binary theorem. In addition, we mapped out a recursive procedure for generating the power set. A brief investigation revealed that Python’s set() class could not accommodate our need to include subsets within a set as in the case of power sets. To solve the problem, we introduced a custom container class with a set-valued attribute, whose instances are “hashable” and thus, eligible for membership in set objects.
Starting with the container strategy from part one, in part two we expanded our custom class, ModSet(), to include methods that perform copying, nesting, uniqueness-filtering, set-union and set-difference operations as well as others. We verified that all ModSet() methods functioned as desired. Many of the methods added would prove necessary for both methods of power set generation to follow.
In part three, we realized our goal of generating power sets. First, we detailed program flow of both the Binary Mask and Recursive approaches of power set generation. The mask routine used list indexing and took more lines of code than recursive method, but called fewer class methods. Our Recursive approach was shorter in terms of lines of code because it incorporated more sibling methods of the ModSet() class. We then explained the control flow of the recursive generator hoping to illustrate how recursive algorithms function. Finally, we compared relative run times of the two approaches. It turned out that, as expected, the Binary Mask routine took less time to run than its recursive counterpart.
Lastly, stay tuned for part foura where we’ll walk-through and test a more efficient algorithm for generating power sets in the ModSet() class.
Sources (part 3)
1. D. Van Dalen; H. C. Doets; H. De Swart (9 May 2014). Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Set Theory for Non Logicians, Working and Teaching Mathematicians and Students. Elsevier Science. ISBN 978-1-4831-5039-0.
2. Recursion (computer science), Recursion versus Iteration, Wikipedia.
The complete ModSet() class
You can download ModSet()‘s complete definition from github: modset.py

The ModSet() class by nullexit.org is licensed under a Creative Commons Attribution 4.0 International License.
Power sets in Python: an object-oriented approach (part 1)
Overview
In this three part series, we will demonstrate how to construct the power set using both iterative and recursive algorithms. You may recall, the power set of a set $S$ is the collection of all (unique) subsets of $S$, including the empty set and $S$ itself. Though Python's set class does not accept its own set objects as members, we will define a new object class, ModSet(), that encapsulates member subsets in hashable containers so that they can be included within set instance, the power set.
Here in part one, we'll use a minimal working example to demonstrate our solution to the subset inclusion problem. Next, in part two, we construct the ModSet() object with all the methods necessary to support power set generation by two distinct approaches. Finally, in part three we develop and run binary mask and recursive routines for generating power sets in Python.
Now, a bit about power sets.
Power sets defined and how to build them
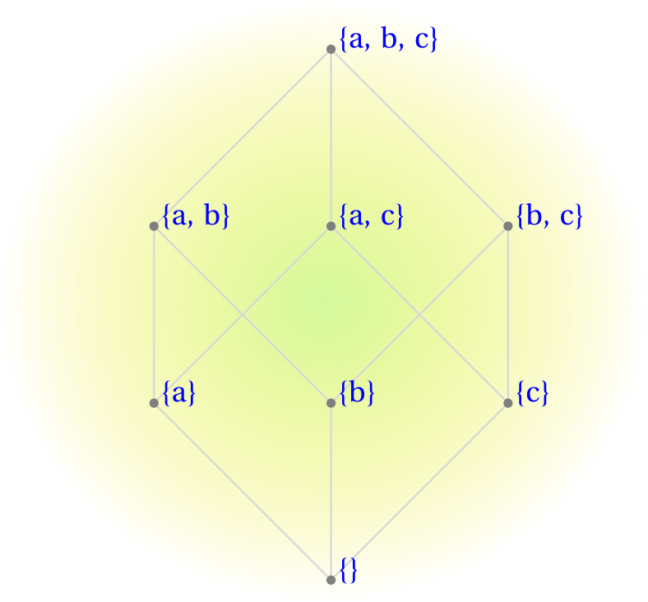
If a set $S$ has $n$ elements, its power set will have $2^n$ member subsets; these include the complete "source" set, $S$ itself, as well as the empty set, $\emptyset$. For example, the power set of set $\{x,y,z\}$ is: $\{\emptyset, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\}, \{x, y, z\}\}$. Please notice that there are $2^3=8$ subset elements, all of which are unique; that is, no two subsets contain the same collection of members.
Why $2^n$? Because all possible subsets can be formed by selecting their members according to digit occurrence in the base-2 integers that count from $0$ to $2^n$
Clear as mud, right? Don't worry, we'll explain.
The Binary Mask approach
Say we have a source set comprised of four members, $\{a,b,c,d\}$. The corresponding mask will have four digits that can each take on values of either $0$ or $1$. If a mask digit equals $1$ we keep the element in the corresponding location of the source set, if a digit is $0$, we reject the corresponding element.
Working with binary masks
Here's an illustrative example: binary mask $0101$ operating on source set $\{a,b,c,d\}$ would form subset member $\{b,d\}$ of the power set. Similarly, binary mask $1110$ selects subset $\{a,b,c\}$. Using the same rule, mask $0000$ selects $\emptyset$, while $1111$ forms the original source set of all four elements. There are $2^4=16$ unique bit combinations in a 4-digit binary mask, so there are $16$ unique member subsets in the power set of a four-element source set. Now, extending this procedure to a set comprised of $n$ elements rather than $4$, you can see that its power set will have $2^n$ member subsets by the same rule (the binomal theorem).
The above procedure may seem to have a certain efficiency and elegance in its directness; in this series, we'll call this method "the Binary Mask approach".
But there is another procedure we can use to build power sets...
A Recursive approach
Alternatively, you can take your source set, $\{a,b,c,d\}$, remove one of its members, $a$, then define a new subset with the members that remain, $\{b,c,d\}$, and include it as a new element in a collection. We apply the same element removal procedure to the resultant subset from the previous step, then to the result of the current step, and to the result of the next step, and so on, until we are left with a result that is empty. If we repeat the removal operation for all members of the starting set and each resultant subset, you will produce the a collection of subsets that includes the power set, with many redundant subsets in the collection as well. We'll address this issue of duplication in the next section.
Recursion walk-through
For example: removing $b$ from our source set leaves subset $\{a,c,d\}$. Removing element $c$ from subset $\{a,c,d\}$ leaves subset $\{a,d\}$. Taking $a$ from subset $\{a,d\}$ results in subset $\{d\}$. And finally, removing element $d$ from subset $\{d\}$ produces the $\emptyset$. Then we go all the way back up to the top, this time taking $c$ from $\{a,b,c,d\}$ and repeat the entire stripping procedure until we are left with $\emptyset$ as above. Next we do the same starting with members $d$ and $a$; repeating the full stripping procedure for each.
Notice that we could have removed any existing member from any set or subset at any step in the process--not only the particular members stated above. For example we could have removed $d$ from subset $\{a,c,d\}$ instead of $c$ at that step. If we explore every possible sequence of element removal, we'll notice that identical subsets can be produced by different sequences (e.g. $\{a,c\}$ results from sequence $\{a,b,c,d\} \rightarrow \{a,b,c\} \rightarrow \{a,c\}$, as well as $\{a,b,c,d\} \rightarrow \{a,c,d\} \rightarrow \{a,c\}$). So, our algorithm will need to exclude non-unique subset candidates from the collection; either as the power set is being populated or by removing duplicates after the entire collection has been formed.
Motivation and next step
This second procedure for generating power sets we'll call "our Recursive approach"1. While our Recursive approach may lack the directness and efficiency of the Binary Mask algorithm, we hope that coding it will at least prove to be an instructive, "chops-building", exercise in recursion, if no other utility can be found for it in the future.
Before we can implement either algorithm, however, we need to investigate the behavior of Python's set() class. Specifically, if it suffices for our purpose of containing subsets within an all-encompassing superset, in our case: the power set.
[Spoiler alert... it doesn't.]
The Python set class
The set class in python takes only immutable types (e.g. strings, numeric values, and tuples) as members. Under the hood, a set() object retains a hash or pointer to an immutable object that is a member.
shinyPrez = set([20.1, 2017, ('alternative', 'facts'), '\"record-setting\"'])
shinyPrez.add('covfefe')
shinyPrez
Something to notice: the ordering of elements in the set's output string does not match their ordering in its definition. Unlike Python's iterable list() class, set() objects do not retain member ordering.
When you try to insert a mutable type, lists or dictionaries for example, Python will spit back an 'unhashable' type error.
shinyPrez.add(['Cambridge', 'Analytica'])
See, no dice. Also, because set() objects are mutable, the same goes if you attempt to include a set as a member of another set.
woopsy = set([('impeachment', 'proceedings')])
woopsy
shinyPrez.add(woopsy)
Though you can join sets together, by combining unique members into a single pool, with the set.union() operation.
shinyPrez = shinyPrez.union(woopsy)
shinyPrez
Class instances can be hashed
Now, because separate instances of a class are allocated their own locations in memory, they are hashable; even if they contain unhashable values as attributes. And, even if the values of the attributes of the two instances are equivalent.
class Advisor():
def __init__(self):
self.val = {'Presidential', 'pardon'} # Attribute contains unhashable set
RogerS = Advisor() # has set for attribute .val
PaulM = Advisor() # has same set as above for its attribute .val
modelCitz = set([PaulM, RogerS]) # include the two instances as members of a set
print(type(modelCitz)) # c is indeed a set
print([type(el) for el in modelCitz]) # members of the set are instances of Advisor class
print([type(el.val) for el in modelCitz]) # attributes of member instances are sets
We adopted the above definition from Max Bernstein's blog. Also, we can instruct that instances of the class, when called, define themselves as their .val attribute (Bernstein, 2019).
class Advisor():
def __init__(self):
self.val = {'Presidential', 'pardon'}
def __repr__(self): # method to generate representative code string
return self.val.__repr__() # return __repr__ code string for the
# Advisor().val attribute
MichaelF = Advisor()
noHarmDone = set([MichaelF])
noHarmDone
A quick look might suggest that we bypassed set()'s exclusion of mutables here. But don't be fooled. While we have the appearance of having a set object contained within another set object, what we actually have is a set that contains a hash to an instance of Advisor() that has a set as an attribute.
print(type(noHarmDone)) # Notice that set()'s lack of indexing
print(type(list(noHarmDone)[0])) # methods can be a bit
print(type(list(noHarmDone)[0].val)) # of a pain..!
Why define a new class?
The skeptical Python programmer at this stage is likely asking her/his/them-self: "why don't you just use a list object rather than defining a whole 'nother class for cryin' out loud!?!" Number 1, lists are not hashable; for our power set generation routines to come, we require a container that is. Number 2, lists permit duplicate entries; enforcing member uniqueness would require more coding. Finally, number 3, lists preserve element ordering; while not a deal-breaker for our purposes, lists do not mathematically qualify as sets for this reason and others.
Plan for part two
In part two, we'll define a new class, ModSet(), that will behave much like Python's set() class, but with an added set-valued attribute. Our ModSet() class will employ the same approach just demonstrated above: use of a hashable class instance to contain unhashable set objects. With these container instances themselves eligible for membership in a super-set() object. Use of ModSet objects will allow us to form an all-encompassing power set that--indirectly--has sub-set() instances as members. More than a cosmetic device, defining a set container class in this way will allow the power set of a given set object to be generated using Binary Mask and Recursion-based algorithms later on in part three.
Sources (part 1)
1. Bernstein, M., Recursive Python Objects, https://bernsteinbear.com/blog. 2019.

