Overview
In this three part series, we will demonstrate how to construct the power set using both iterative and recursive algorithms. You may recall, the power set of a set $S$ is the collection of all (unique) subsets of $S$, including the empty set and $S$ itself. Though Python's set class does not accept its own set objects as members, we will define a new object class, ModSet(), that encapsulates member subsets in hashable containers so that they can be included within set instance, the power set.
Here in part one, we'll use a minimal working example to demonstrate our solution to the subset inclusion problem. Next, in part two, we construct the ModSet() object with all the methods necessary to support power set generation by two distinct approaches. Finally, in part three we develop and run binary mask and recursive routines for generating power sets in Python.
Now, a bit about power sets.
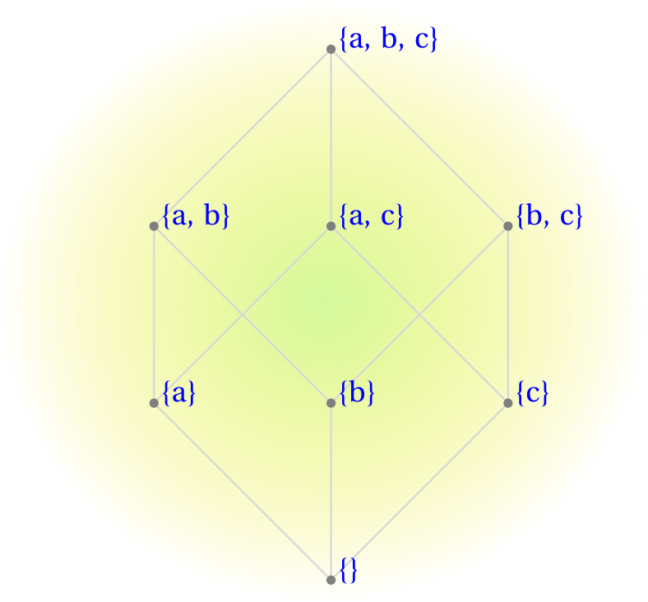
Power sets defined and how to build them
If a set $S$ has $n$ elements, its power set will have $2^n$ member subsets; these include the complete "source" set, $S$ itself, as well as the empty set, $\emptyset$. For example, the power set of set $\{x,y,z\}$ is: $\{\emptyset, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\}, \{x, y, z\}\}$. Please notice that there are $2^3=8$ subset elements, all of which are unique; that is, no two subsets contain the same collection of members.
Why $2^n$? Because all possible subsets can be formed by selecting their members according to digit occurrence in the base-2 integers that count from $0$ to $2^n$
Clear as mud, right? Don't worry, we'll explain.
The Binary Mask approach
Say we have a source set comprised of four members, $\{a,b,c,d\}$. The corresponding mask will have four digits that can each take on values of either $0$ or $1$. If a mask digit equals $1$ we keep the element in the corresponding location of the source set, if a digit is $0$, we reject the corresponding element.
Working with binary masks
Here's an illustrative example: binary mask $0101$ operating on source set $\{a,b,c,d\}$ would form subset member $\{b,d\}$ of the power set. Similarly, binary mask $1110$ selects subset $\{a,b,c\}$. Using the same rule, mask $0000$ selects $\emptyset$, while $1111$ forms the original source set of all four elements. There are $2^4=16$ unique bit combinations in a 4-digit binary mask, so there are $16$ unique member subsets in the power set of a four-element source set. Now, extending this procedure to a set comprised of $n$ elements rather than $4$, you can see that its power set will have $2^n$ member subsets by the same rule (the binomal theorem).
The above procedure may seem to have a certain efficiency and elegance in its directness; in this series, we'll call this method "the Binary Mask approach".
But there is another procedure we can use to build power sets...
A Recursive approach
Alternatively, you can take your source set, $\{a,b,c,d\}$, remove one of its members, $a$, then define a new subset with the members that remain, $\{b,c,d\}$, and include it as a new element in a collection. We apply the same element removal procedure to the resultant subset from the previous step, then to the result of the current step, and to the result of the next step, and so on, until we are left with a result that is empty. If we repeat the removal operation for all members of the starting set and each resultant subset, you will produce the a collection of subsets that includes the power set, with many redundant subsets in the collection as well. We'll address this issue of duplication in the next section.
Recursion walk-through
For example: removing $b$ from our source set leaves subset $\{a,c,d\}$. Removing element $c$ from subset $\{a,c,d\}$ leaves subset $\{a,d\}$. Taking $a$ from subset $\{a,d\}$ results in subset $\{d\}$. And finally, removing element $d$ from subset $\{d\}$ produces the $\emptyset$. Then we go all the way back up to the top, this time taking $c$ from $\{a,b,c,d\}$ and repeat the entire stripping procedure until we are left with $\emptyset$ as above. Next we do the same starting with members $d$ and $a$; repeating the full stripping procedure for each.
Notice that we could have removed any existing member from any set or subset at any step in the process--not only the particular members stated above. For example we could have removed $d$ from subset $\{a,c,d\}$ instead of $c$ at that step. If we explore every possible sequence of element removal, we'll notice that identical subsets can be produced by different sequences (e.g. $\{a,c\}$ results from sequence $\{a,b,c,d\} \rightarrow \{a,b,c\} \rightarrow \{a,c\}$, as well as $\{a,b,c,d\} \rightarrow \{a,c,d\} \rightarrow \{a,c\}$). So, our algorithm will need to exclude non-unique subset candidates from the collection; either as the power set is being populated or by removing duplicates after the entire collection has been formed.
Motivation and next step
This second procedure for generating power sets we'll call "our Recursive approach"1. While our Recursive approach may lack the directness and efficiency of the Binary Mask algorithm, we hope that coding it will at least prove to be an instructive, "chops-building", exercise in recursion, if no other utility can be found for it in the future.
Before we can implement either algorithm, however, we need to investigate the behavior of Python's set() class. Specifically, if it suffices for our purpose of containing subsets within an all-encompassing superset, in our case: the power set.
[Spoiler alert... it doesn't.]
The Python set class
The set class in python takes only immutable types (e.g. strings, numeric values, and tuples) as members. Under the hood, a set() object retains a hash or pointer to an immutable object that is a member.
shinyPrez = set([20.1, 2017, ('alternative', 'facts'), '\"record-setting\"'])
shinyPrez.add('covfefe')
shinyPrez
Something to notice: the ordering of elements in the set's output string does not match their ordering in its definition. Unlike Python's iterable list() class, set() objects do not retain member ordering.
When you try to insert a mutable type, lists or dictionaries for example, Python will spit back an 'unhashable' type error.
shinyPrez.add(['Cambridge', 'Analytica'])
See, no dice. Also, because set() objects are mutable, the same goes if you attempt to include a set as a member of another set.
woopsy = set([('impeachment', 'proceedings')])
woopsy
shinyPrez.add(woopsy)
Though you can join sets together, by combining unique members into a single pool, with the set.union() operation.
shinyPrez = shinyPrez.union(woopsy)
shinyPrez
Class instances can be hashed
Now, because separate instances of a class are allocated their own locations in memory, they are hashable; even if they contain unhashable values as attributes. And, even if the values of the attributes of the two instances are equivalent.
class Advisor():
def __init__(self):
self.val = {'Presidential', 'pardon'} # Attribute contains unhashable set
RogerS = Advisor() # has set for attribute .val
PaulM = Advisor() # has same set as above for its attribute .val
modelCitz = set([PaulM, RogerS]) # include the two instances as members of a set
print(type(modelCitz)) # c is indeed a set
print([type(el) for el in modelCitz]) # members of the set are instances of Advisor class
print([type(el.val) for el in modelCitz]) # attributes of member instances are sets
We adopted the above definition from Max Bernstein's blog. Also, we can instruct that instances of the class, when called, define themselves as their .val attribute (Bernstein, 2019).
class Advisor():
def __init__(self):
self.val = {'Presidential', 'pardon'}
def __repr__(self): # method to generate representative code string
return self.val.__repr__() # return __repr__ code string for the
# Advisor().val attribute
MichaelF = Advisor()
noHarmDone = set([MichaelF])
noHarmDone
A quick look might suggest that we bypassed set()'s exclusion of mutables here. But don't be fooled. While we have the appearance of having a set object contained within another set object, what we actually have is a set that contains a hash to an instance of Advisor() that has a set as an attribute.
print(type(noHarmDone)) # Notice that set()'s lack of indexing
print(type(list(noHarmDone)[0])) # methods can be a bit
print(type(list(noHarmDone)[0].val)) # of a pain..!
Why define a new class?
The skeptical Python programmer at this stage is likely asking her/his/them-self: "why don't you just use a list object rather than defining a whole 'nother class for cryin' out loud!?!" Number 1, lists are not hashable; for our power set generation routines to come, we require a container that is. Number 2, lists permit duplicate entries; enforcing member uniqueness would require more coding. Finally, number 3, lists preserve element ordering; while not a deal-breaker for our purposes, lists do not mathematically qualify as sets for this reason and others.
Plan for part two
In part two, we'll define a new class, ModSet(), that will behave much like Python's set() class, but with an added set-valued attribute. Our ModSet() class will employ the same approach just demonstrated above: use of a hashable class instance to contain unhashable set objects. With these container instances themselves eligible for membership in a super-set() object. Use of ModSet objects will allow us to form an all-encompassing power set that--indirectly--has sub-set() instances as members. More than a cosmetic device, defining a set container class in this way will allow the power set of a given set object to be generated using Binary Mask and Recursion-based algorithms later on in part three.
Sources (part 1)
1. Bernstein, M., Recursive Python Objects, https://bernsteinbear.com/blog. 2019.